Fit a Mean Parametrized Conway-Maxwell Poisson Generalized Linear Model

Source: R/glm.cmp.R

The function glm.cmp is used to fit a mean parametrized Conway-Maxwell Poisson generalized linear model with a log-link by using Fisher Scoring iteration.

glm.cmp(
  formula,
  formula_nu = NULL,
  data,
  offset = NULL,
  subset,
  na.action,
  betastart = NULL,
  gammastart = NULL,
  lambdalb = 1e-10,
  lambdaub = 1000,
  maxlambdaiter = 1000,
  tol = 1e-06,
  contrasts_mu = NULL,
  contrasts_nu = NULL
)

Arguments

formula

an object of class 'formula': a symbolic description of the model to be fitted to the mean via log-link.

formula_nu

an optional object of class 'formula': a symbolic description of the model to be fitted to the dispersion via log-link.

data

an optional data frame containing the variables in the model

offset

this can be used to specify an a priori known component to be included in the linear predictor for mean during fitting. This should be NULL or a numeric vector of length equal to the number of cases.

subset

an optional vector specifying a subset of observations to be used in the fitting process.

na.action

a function which indicates what should happen when the data contain NAs. The default is set by the na.action setting of options, and is na.fail if that is unset. The ‘factory-fresh’ default is na.omit. Another possible value is NULL, no action. Value na.exclude can be useful.

betastart

starting values for the parameters in the linear predictor for mu.

gammastart

starting values for the parameters in the linear predictor for nu.

lambdalb, lambdaub

numeric: the lower and upper end points for the interval to be searched for lambda(s). The default value for lambdaub should be sufficient for small to moderate size nu. If nu is large and required a larger lambdaub, the algorithm will scale up lambdaub accordingly.

maxlambdaiter

numeric: the maximum number of iterations allowed to solve for lambda(s).

tol

numeric: the convergence threshold. A lambda is said to satisfy the mean constraint if the absolute difference between the calculated mean and a fitted values is less than tol.

contrasts_mu, contrasts_nu

optional lists. See the contrasts.arg of model.matrix.default.

Value

A fitted model object of class cmp similar to one obtained from glmor glm.nb. The function summary (i.e., summary.cmp) can be used to obtain and print a summary of the results. The functions plot (i.e., plot.cmp) and gg_plot can be used to produce a range of diagnostic plots. The generic assessor functions coef (i.e., coef.cmp), logLik (i.e., logLik.cmp) fitted (i.e., fitted.cmp), nobs (i.e., nobs.cmp), AIC (i.e., AIC.cmp) and residuals (i.e., residuals.cmp) can be used to extract various useful features of the value returned by glm.cmp. The functions LRTnu and cmplrtest can be used to perform a likelihood ratio chi-squared test for nu = 1 and for nested COM-Poisson model respectively. An object class 'glm.cmp' is a list containing at least the following components:

coefficients

a named vector of coefficients

coefficients_beta

a named vector of mean coefficients

coefficients_gamma

a named vector of dispersion coefficients

se_beta

approximate standard errors (using observed rather than expected information) for mean coefficients

se_gamma

approximate standard errors (using observed rather than expected information) for dispersion coefficients

residuals

the response residuals (i.e., observed-fitted)

fitted_values

the fitted mean values

rank_mu

the numeric rank of the fitted linear model for mean

rank_nu

the numeric rank of the fitted linear model for dispersion

linear_predictors

the linear fit for mean on log scale

df_residuals

the residuals degrees of freedom

df_null

the residual degrees of freedom for the null model

null_deviance

The deviance for the null model. The null model will include only the intercept.

deviance; residual_deviance

The residual deviance of the model

y

the y vector used.

x

the model matrix for mean

s

the model matrix for dispersion

model_mu

the model frame for mu

model_nu

the model frame for nu

call

the matched call

formula

the formula supplied for mean

formula_nu

the formula supplied for dispersion

terms_mu

the terms object used for mean

terms_nu

the terms object used for dispersion

data

the data argument

offset

the offset vector used

lambdaub

the final lambdaub used

Details

Fit a mean-parametrized COM-Poisson regression using maximum likelihood estimation via an iterative Fisher Scoring algorithm.

Currently, the COM-Poisson regression model allows constant dispersion and regression being linked to the dispersion parameter i.e. varying dispersion.

For the constant dispersion model, the model is

$$Y_i \sim CMP(\mu_i, \nu),$$

where

$$E(Y_i) = \mu_i = exp(x_i^{\top} \beta),$$

and \(\nu > 0\) is the dispersion parameter.

The fitted COM-Poisson distribution is over- or under-dispersed if \(\nu < 1\) and \(\nu > 1\) respectively.

For the varying dispersion model, the model is

$$Y_i \sim CMP(\mu_i, \nu_i),$$

where

$$E(Y_i) = \mu_i = exp(x_i^{\top} \beta),$$

and dispersion parameters are model via

$$\nu_i = exp(s_i^{\top} \gamma),$$

where \(x_i\) and \(s_i\) are some covariates.

References

Fung, T., Alwan, A., Wishart, J. and Huang, A. (2020). mpcmp: Mean-parametrized Conway-Maxwell Poisson Regression. R package version 0.3.4.

Huang, A. (2017). Mean-parametrized Conway-Maxwell-Poisson regression models for dispersed counts. Statistical Modelling 17, 359--380.

See also

summary.cmp, autoplot.cmp, plot.cmp, fitted.cmp, residuals.cmp and LRTnu.

Additional examples may be found in fish, takeoverbids, cottonbolls.

Examples

### Huang (2017) Page 368--370: Overdispersed Attendance data
data(attendance)
M.attendance <- glm.cmp(daysabs ~ gender + math + prog, data = attendance)
M.attendance
#> 
#> Call: glm.cmp(formula = daysabs ~ gender + math + prog, data = attendance)
#> 
#> Linear Model Coefficients:
#>    (Intercept)      gendermale            math    progAcademic  progVocational  
#>       2.714600       -0.214720       -0.006323       -0.425320       -1.253900  
#> 
#> Dispersion (nu): 0.0202
#> Degrees of Freedom: 313 Total (i.e. Null);  309 Residual
#> Null Deviance: 455.8327 
#> Residual Deviance: 
#> AIC: 1739.026 
#> 
summary(M.attendance)
#> 
#> Call: glm.cmp(formula = daysabs ~ gender + math + prog, data = attendance)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -2.1925  -1.1166  -0.3973   0.2964   2.8154  
#> 
#> Linear Model Coefficients:
#>                 Estimate   Std.Err Z value Pr(>|z|)    
#> (Intercept)     2.714645  0.190407  14.257  < 2e-16 ***
#> gendermale     -0.214720  0.117148  -1.833  0.06682 .  
#> math           -0.006323  0.002386  -2.650  0.00804 ** 
#> progAcademic   -0.425322  0.169525  -2.509  0.01211 *  
#> progVocational -1.253896  0.189478  -6.618 3.65e-11 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> (Dispersion parameter for Mean-CMP estimated to be 0.02024)
#> 
#> 
#>     Null deviance: 455.83  on 313 degrees of freedom
#> Residual deviance: 377.44  on 309 degrees of freedom
#> 
#> AIC: 1739.026 
#> 
# \donttest{
plot(M.attendance) # or autoplot(M.attendance)




# }

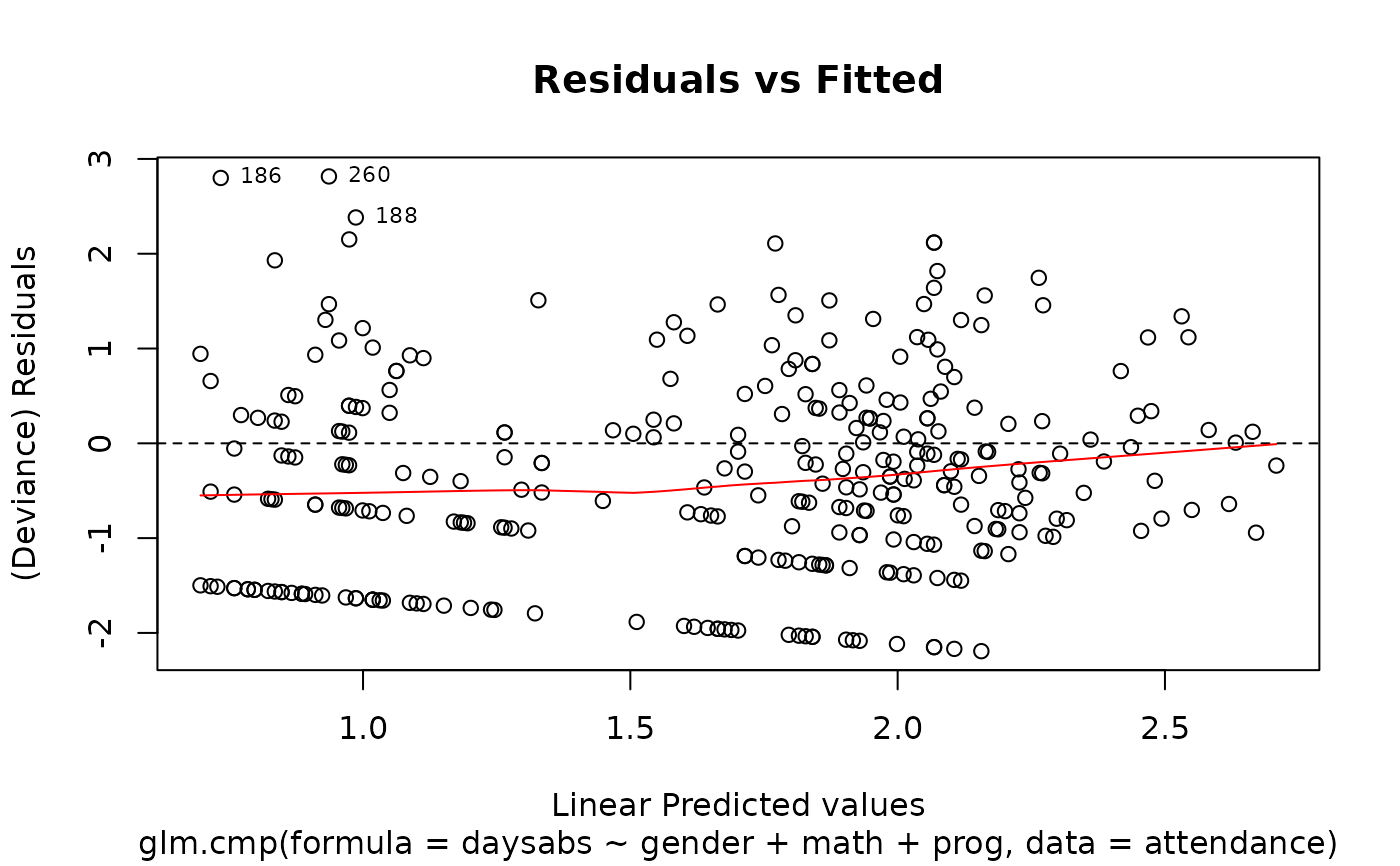
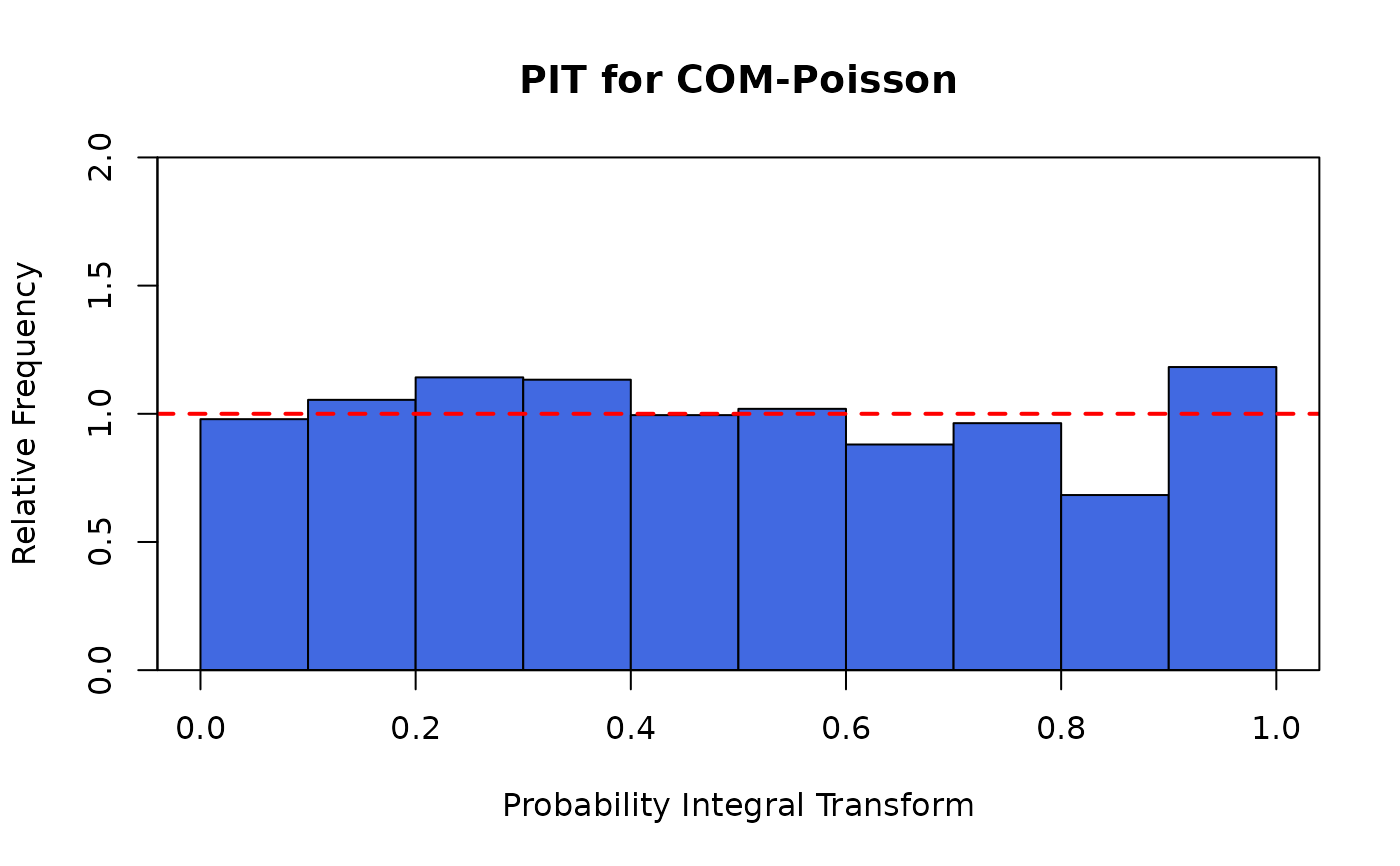
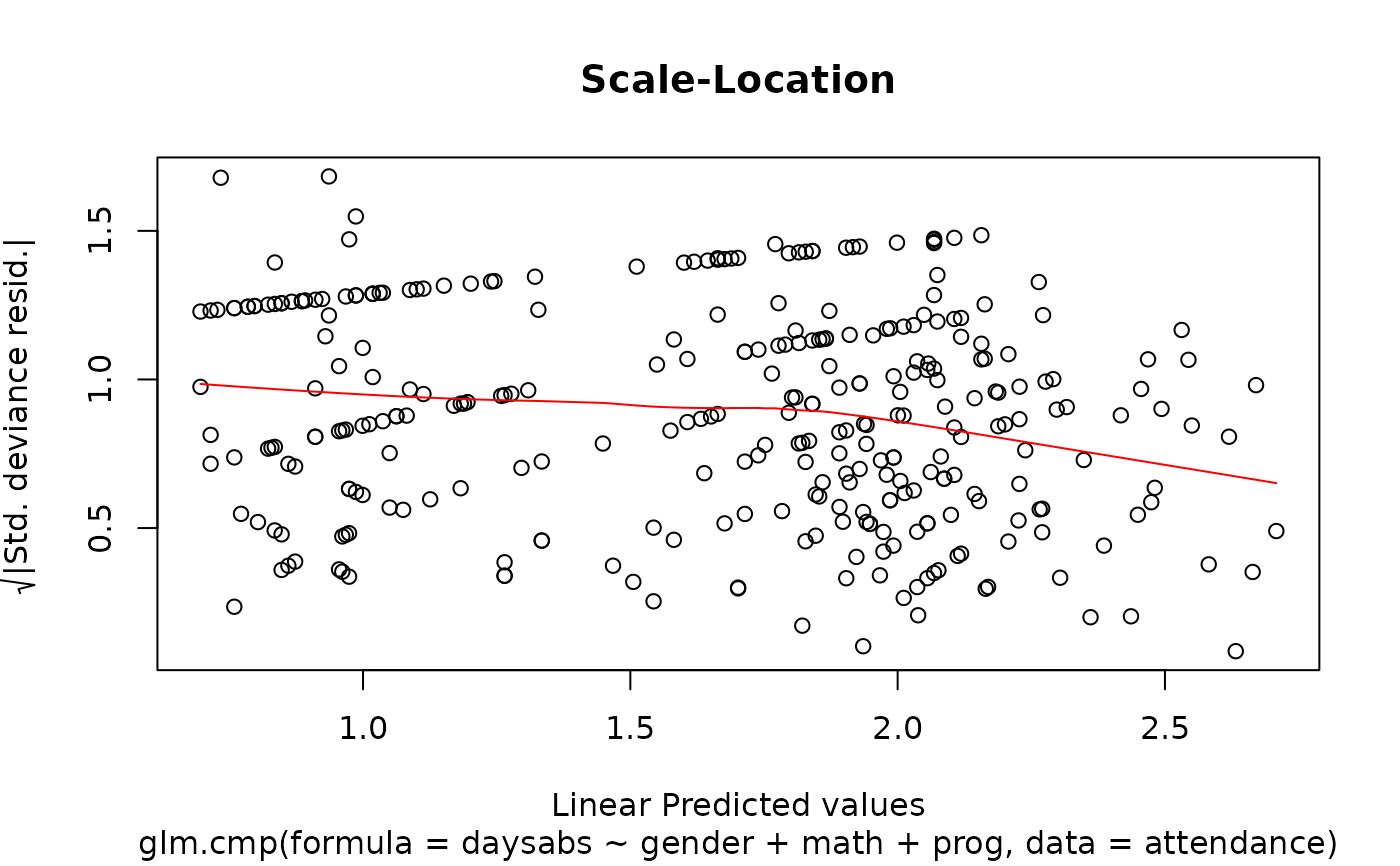
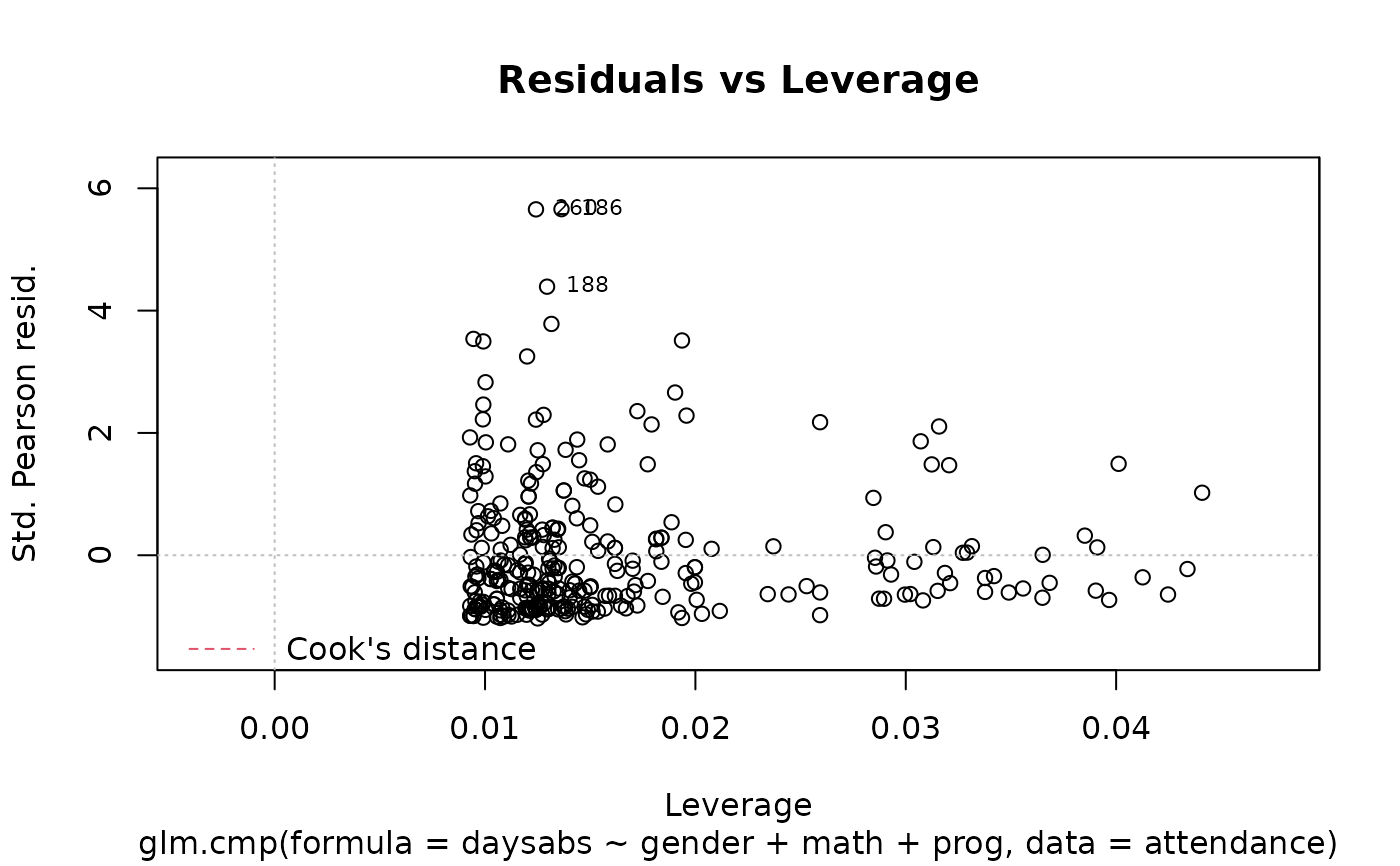### Ribeiro et al. (2013): Varying dispersion as a function of covariates
# \donttest{
data(sitophilus)
M.sit <- glm.cmp(formula = ninsect ~ extract, formula_nu = ~extract, data = sitophilus)
summary(M.sit)
#> 
#> Call: glm.cmp(formula = ninsect ~ extract, formula_nu = ~extract, data = sitophilus)
#> 
#> Deviance Residuals: 
#>      Min        1Q    Median        3Q       Max  
#> -2.21085  -1.16849   0.07494   0.64152   1.72653  
#> 
#> Mean Model Coefficients:
#>                Estimate   Std.Err Z value Pr(>|z|)    
#> (Intercept)    3.449988  0.077974  44.245   <2e-16 ***
#> extractLeaf   -0.006369  0.122139  -0.052    0.958    
#> extractBranch -0.052129  0.123387  -0.422    0.673    
#> extractSeed   -3.354677  0.362108  -9.264   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Dispersion Model Coefficients:
#>               Estimate Std.Err Z value Pr(>|z|)
#> (Intercept)    -0.6652  0.4573  -1.455    0.146
#> extractLeaf    -0.3831  0.6509  -0.589    0.556
#> extractBranch  -0.3724  0.6514  -0.572    0.567
#> extractSeed    -0.1176  1.5461  -0.076    0.939
#> 
#>     Null deviance: 257.211  on 39 degrees of freedom
#> Residual deviance:  41.679  on 32 degrees of freedom
#> 
#> AIC: 260.8279 
#> 
# }